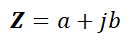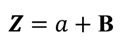INTRODUCTIONWhen confronted with projects that require impedance analysis, the
engineer has no better friend than Microsoft Excel. Here, I'll show
how to make sense of impedance magnitude and phase angle measurements and
how Excel can be used to generate a Nyquist plot like the one shown above.
Note that measuring the complex impedance of a loudspeaker system, across a
range of frequencies, requires dedicated measurement hardware. This
brief doesn't consider how to measure the impedance but assumes that
frequency dependent impedance magnitude and phase angle data is available
for analysis.
Where impedance analysis has value is in modeling
loudspeaker system behavior. For instance, a simulation model of a
loudspeaker system can be assessed for accuracy by comparing a Nyquist plot
of the simulated response to the same measured experimentally.
IMPEDANCEAudio amplifiers are AC voltage sources.
They provide a voltage across the loudspeaker terminals and the loudspeaker
responds by drawing current from the amplifier in proportion to the
magnitude of the applied voltage. The amplitude of the sourced voltage
should be "stiff" meaning the voltage amplitude does not change regardless
of the load presented to the terminals. Stating that a bit
differently, the impedance presented to the amplifier by the load must be
significantly larger than the internal source impedance of the amplifier.
For reactive loads that
store energy such as inductors, capacitors, loudspeakers and crossover
networks, the instantaneous current amplitude will change as a function of
frequency as does the phase relationship between the applied voltage and the
current provided.
The relationship between voltage sourced and current drawn is determined by
the impedance. The current can either lead or lag the
voltage and the magnitude of the lead or lag is measured by the phase angle.
Referenced to voltage, a positive phase angle indicates an inductive
reactance whilst a negative phase angle indicates a capacitive
reactance.
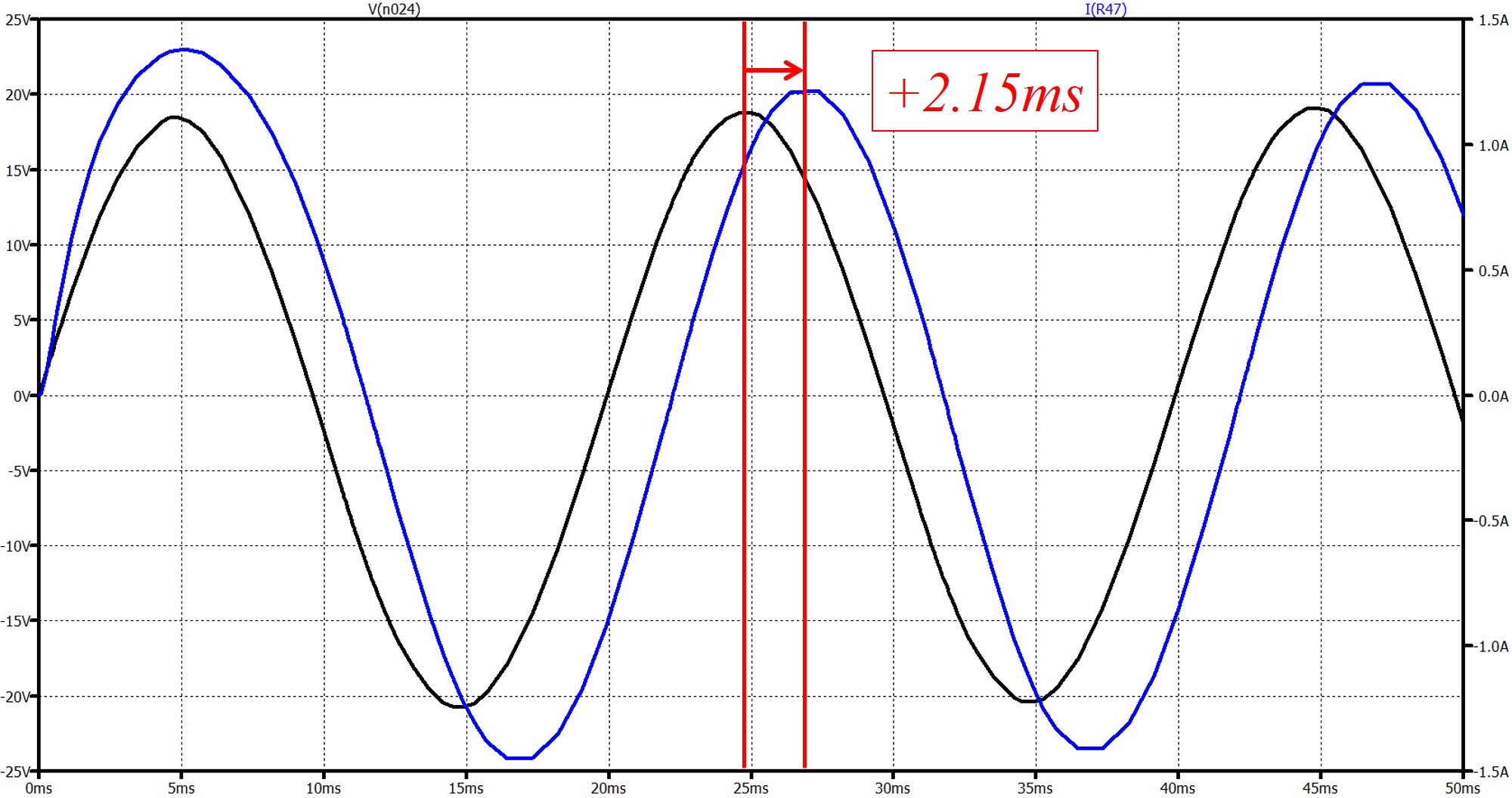
Here's an example. The plot shown below is a
simulation of an audio amplifier output with a reactive load across its output
terminals. The black trace is a 50Hz sine wave with an 18V
amplitude applied to the load. The current waveform provided by the
amplifier is shown
in blue. After a few milliseconds of being turned on, the current
waveform stabilizes to lead the voltage by 2.15ms. Given that it takes 20ms
for a 50Hz sine wave to sweep through a single cycle (=360°), a 2.15ms
leading current waveform
corresponds to approximately a +39° (=+0.69 radians) phase angle between
the two when referenced to the voltage.
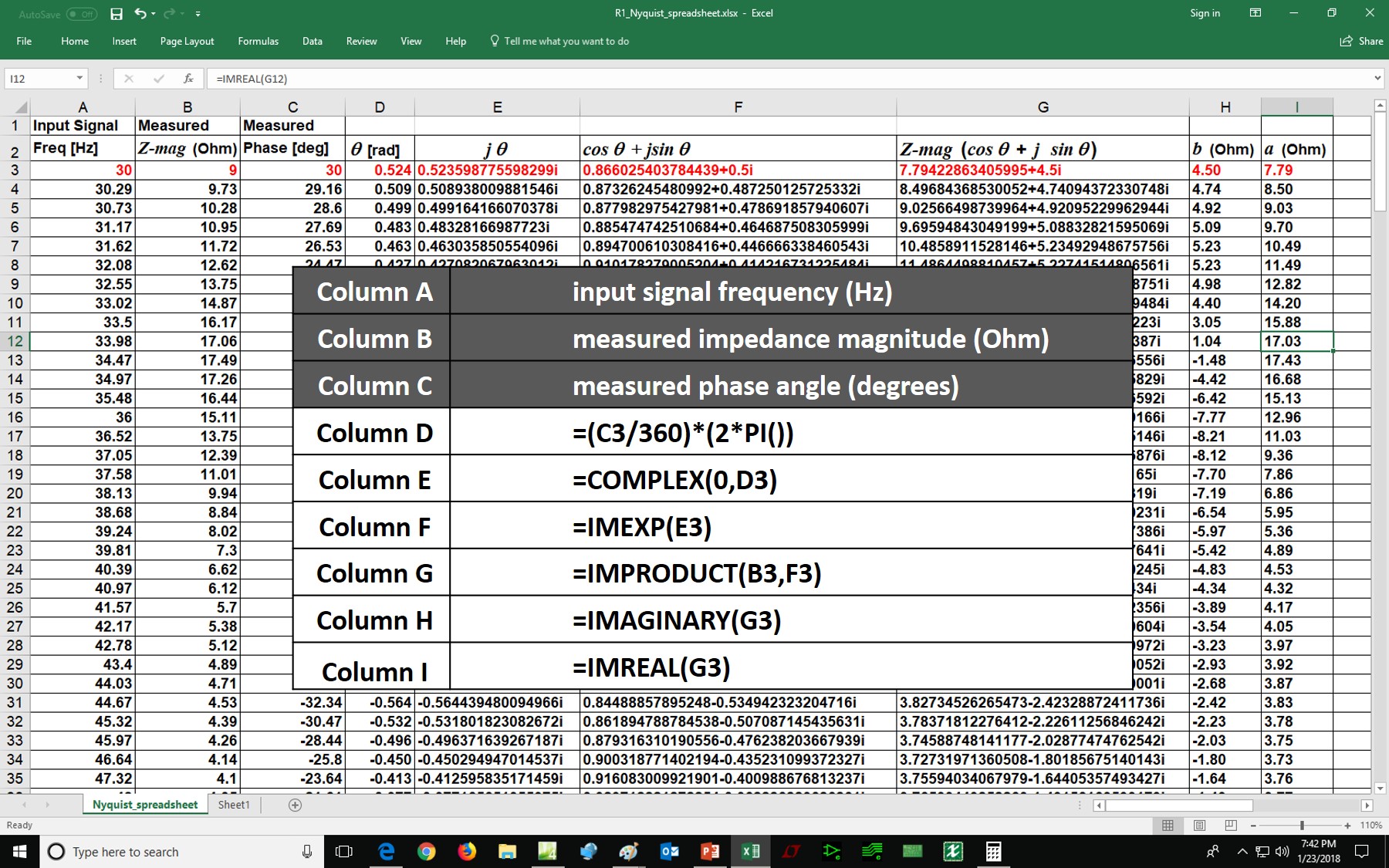
The relationship stated by the "Sparky" cartoon character is the
polar (or exponential) expression of impedance,
Z,
and consists of
the product of a scalar,
Z, and a
exponential function of the phase angle,
q. It looks
complicated but it's not. Impedance can also be expressed using the
rectangular (or Cartesian) form:
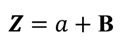 where
a is
the resistance (a positive real number) and
B
is the reactance (an imaginary number) which can take on values of +jX,
-jX
or 0.
where
a is
the resistance (a positive real number) and
B
is the reactance (an imaginary number) which can take on values of +jX,
-jX
or 0.
In the plot shown above, I'll
show how the impedance of the load at 50Hz is determined. But first,
the Nyquist plot is explained.
RECTANGULAR (CARTESIAN) AND POLAR (EXPONENTIAL) FORMS OF IMPEDANCE
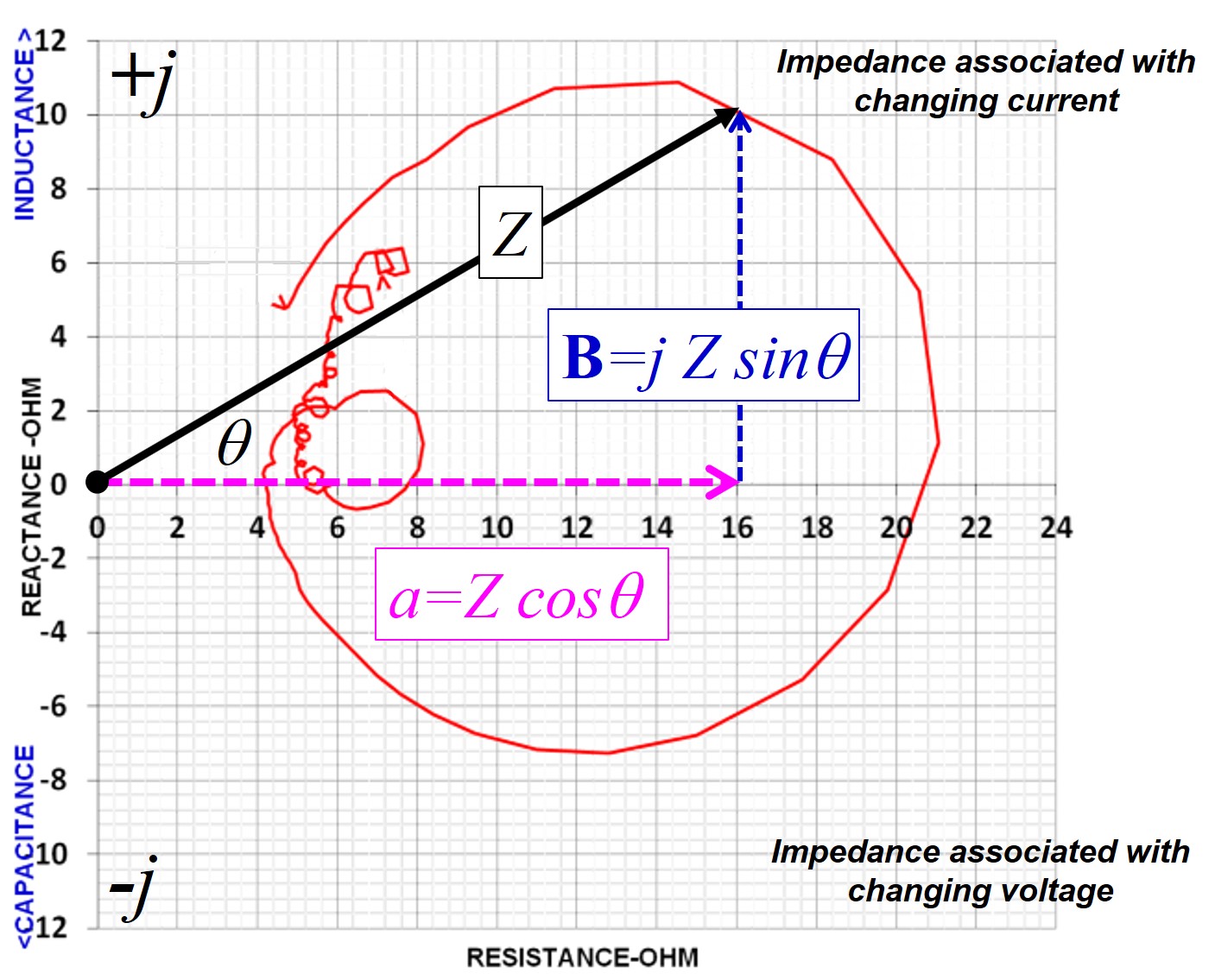
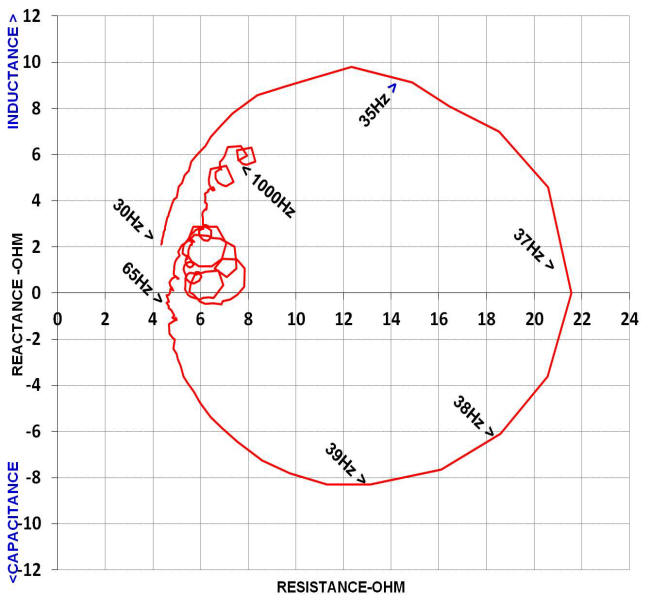
With regard to loudspeaker and audio filter engineering, the "nuts and
bolts" of a Nyquist plot are shown below. The red trace is
the impedance of a Klipschorn bass horn with no crossover filter between it
and the amplifier. The trace represents the impedance plot between a
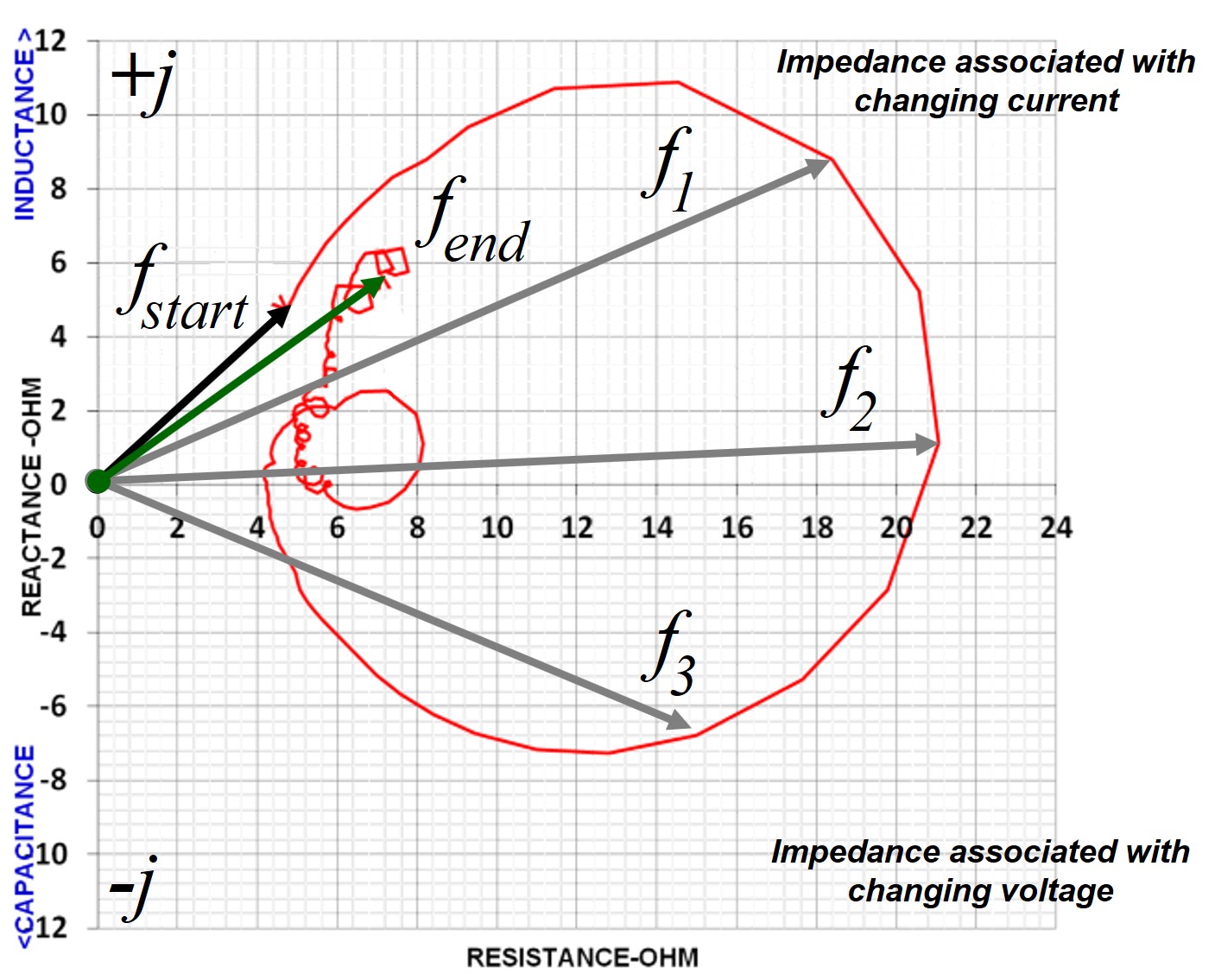
start and end frequency. The black vector labeled
Z has one end anchored at the origin and represents the hypotenuse of a
right triangle with one leg projected along the X-axis (the real axis) and one leg
parallel to
j-axis (the
imaginary axis). The location of the opposite end (arrowhead end) of the
vector is determined by frequency and, as is shown in the adjacent plot,
traces out the impedance continuously as the frequency is increased from the
start to the end of the frequency range examined (
fstart
<
f1 <
f2 <
f3 <
fend). In the case of the Klipschorn plot shown the
start frequency was 30Hz and the end frequency was 1000Hz. The
length of the
Z vector represents
the impedance
magnitude, the
B
leg represents the reactance and the
a leg represents the resistance.
The trigonometric forms of
B
and
a are also shown.
Let's restate the exponential form of
impedance:
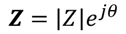 .
.
Using the Euler relationship, the exponential function of phase angle can be expanded:
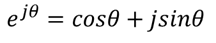
and, when substituted back into the
exponential form and multiplied by IZI, becomes:
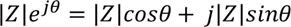
which demonstrates the exponential form
of the impedance consists of the sum of a real and imaginary number.
Thus, by observation and comparison to the rectangular form:
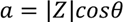
and
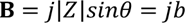 .
.
Thus, the rectangular form of the
impedance is equal to:
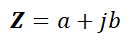
or
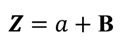
and that's it for the equations.
THE j-OPERATOR
Consider the j-operator as a
mathematical means to keep track of the type of reactance being sensed by
the amplifier. A +j indicates an impedance
associated with changes in current (inductive) whilst
-j indicates impedance associated
with changes in voltage (capacitive).
For example, a reactance of -j4.9
Ohms indicates that the current drawn by the load will lag the voltage
provided by the amplifier and the load presents an impedance to the voltage
source equal to 4.9 Ohms. To associate that to an "equivalent"
capacitance however, the frequency must be known and a perfect 32.5uF capacitor would provide the
4.9 Ohms of reactance at 1000Hz (to
prove it, go to any of a number of "reactance calculators" on the web
that treat both capacitive and inductive loads). At 5000Hz, a 6.5uF
capacitor would also provide 4.9 Ohms of reactance. And that's why
it's
called reactance, the magnitude changes as the frequency changes.
In reality,
capacitors also present a resistance that's independent of frequency but
let's ignore that.
SOME EXAMPLES
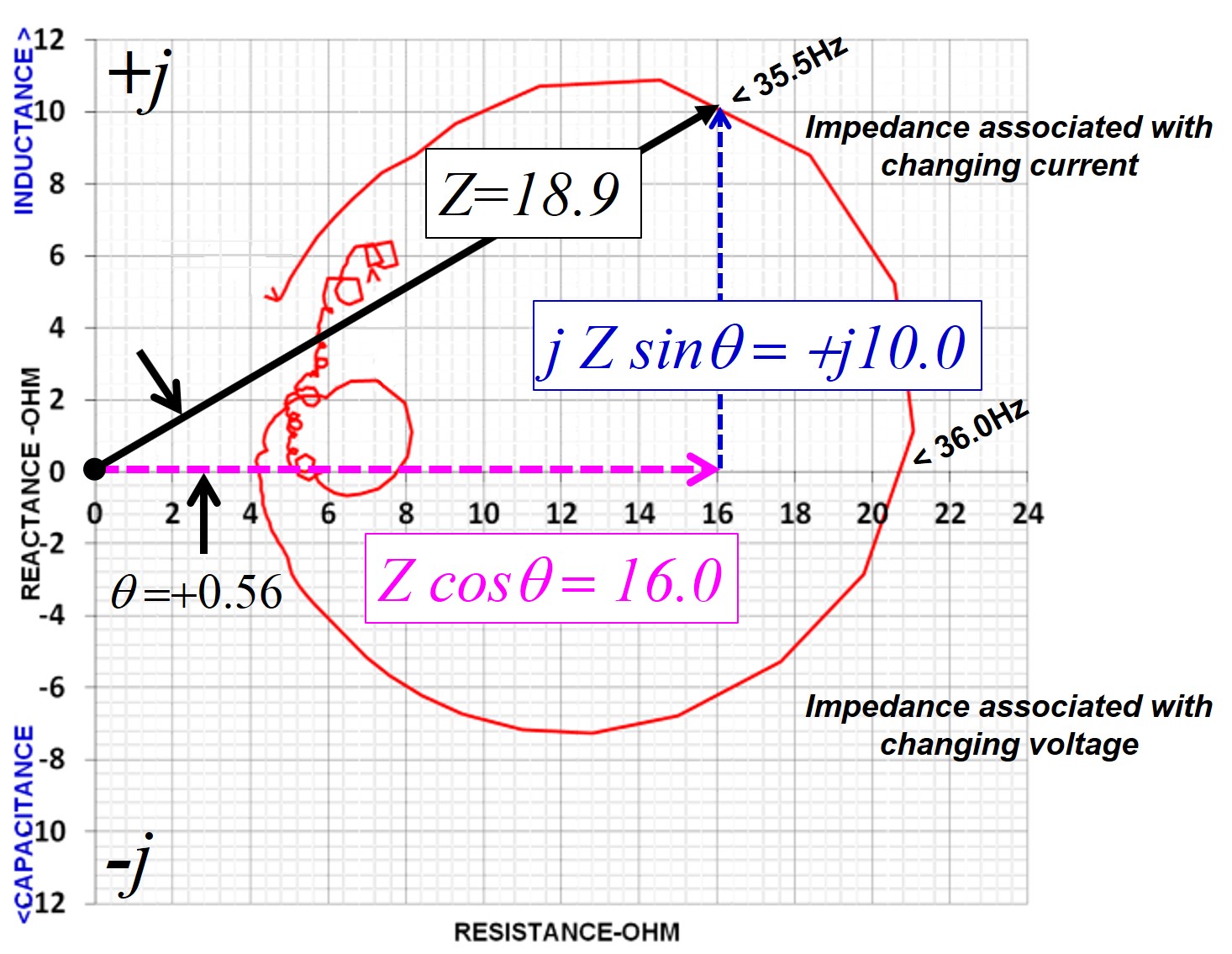
Below are two examples showing how to read the impedance directly from the
Nyquist plot. In the first, the magnitude vector is in the inductive
(+j) quadrant and in the second plot the vector is in the capacitive
(-j) quadrant.
In the first, the magnitude of the impedance at 35.5Hz is 18.9 Ohms and consists
of a 16 Ohm resistance and +
j10.0
Ohm reactance. Expressed in rectangular form the impedance is
Z
= (16 +
j10.0)
Ohms at a frequency of 35.5Hz.
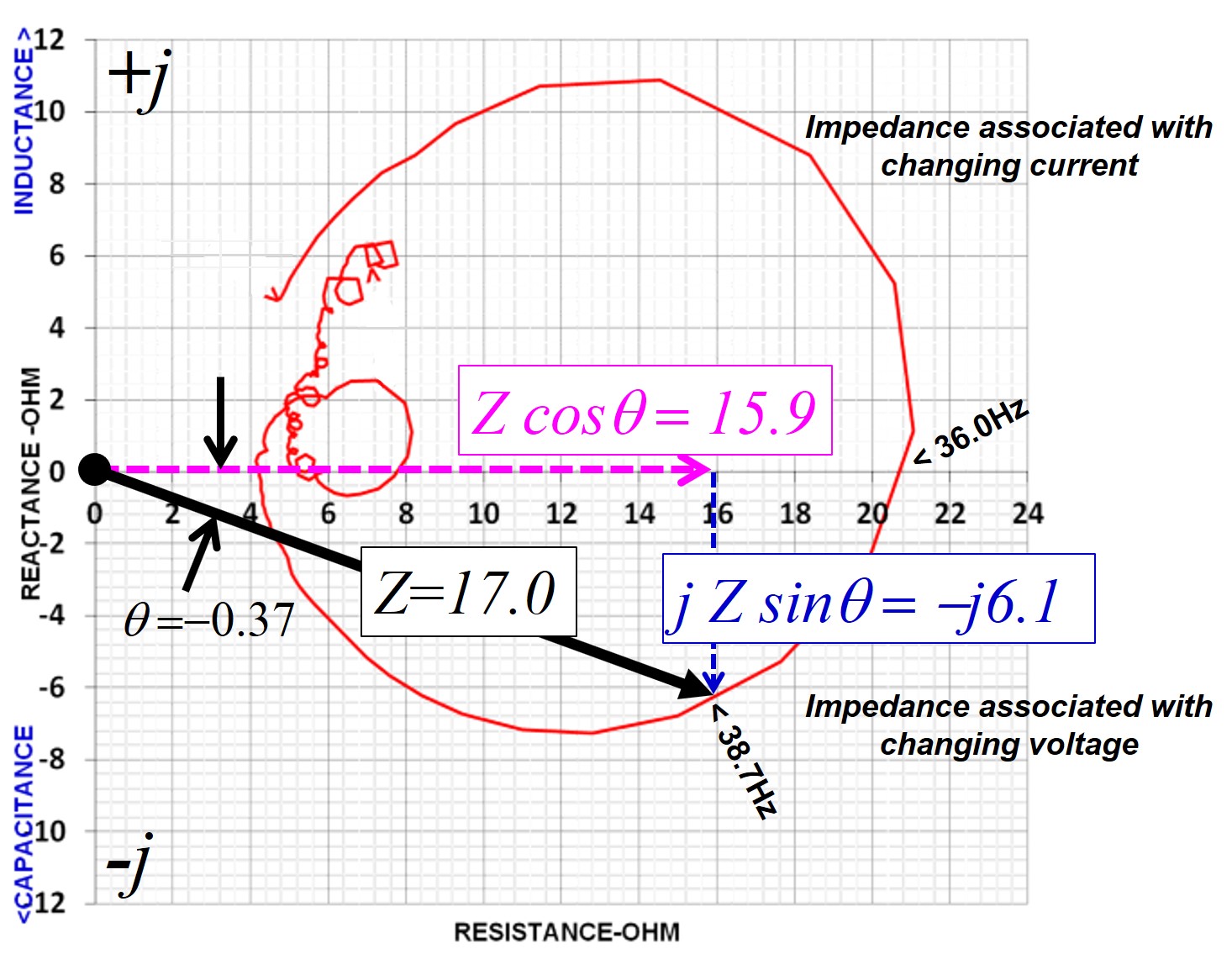
In the second plot, the magnitude
vector is capacitive and has a magnitude of 17 Ohm, the
resistance is 15.9 Ohm and the reactance is
-
j6.1
Ohm and, expressed in rectangular form, is
Z = (15.9 - j6.1)
Ohms at a frequency of 38.7Hz.
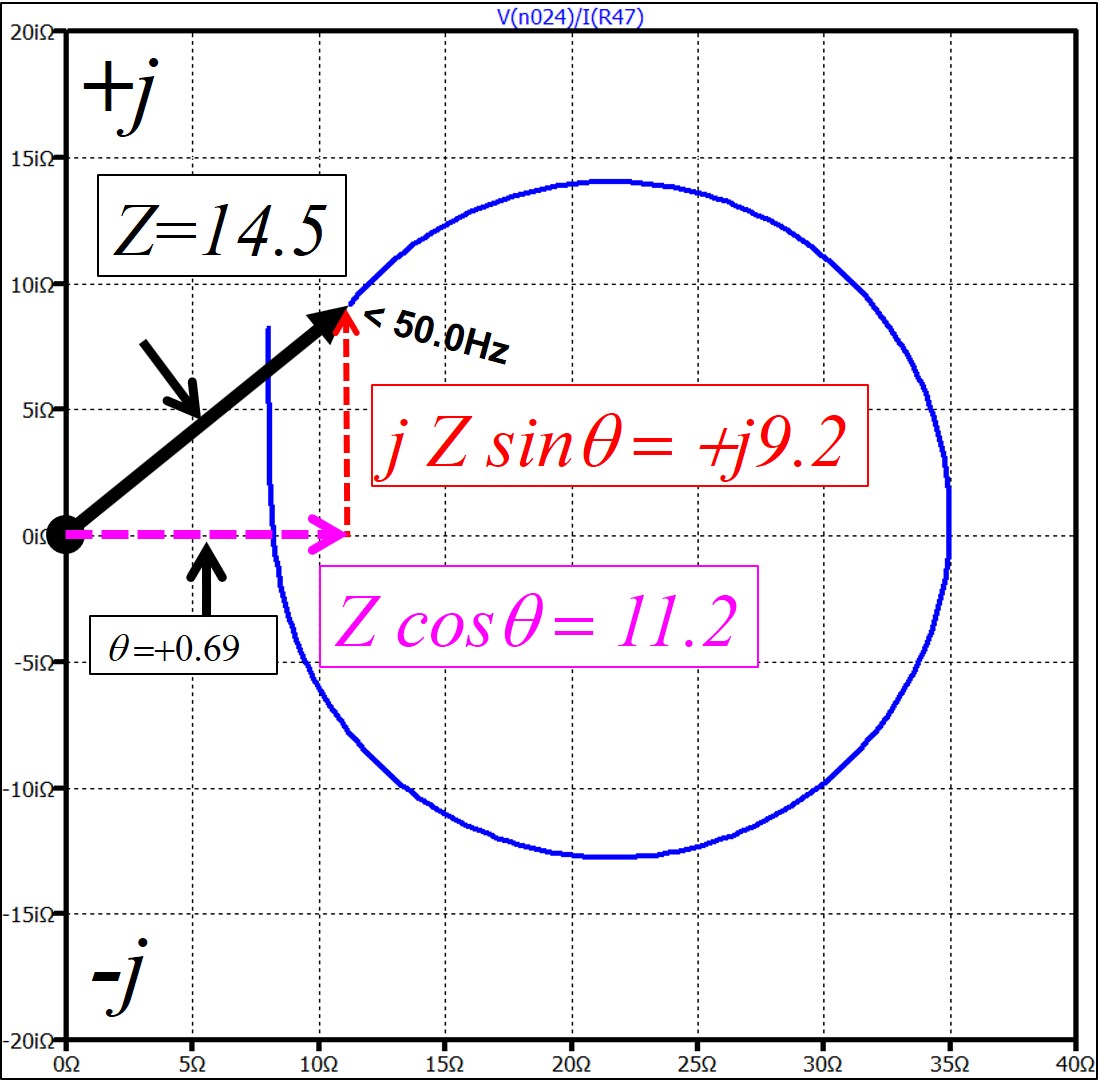
Now consider the impedance of the amplifier simulation shown earlier.
Below is the simulated Nyquist plot of the impedance across the amplifier
terminals between 50 and 1000Hz. At 50Hz the resistive part is 11.2
Ohm and the reactive part is +
j9.2.
The magnitude at 50Hz is 14.6 Ohms and the phase angle is +0.69 radians.
USING EXCEL
Mathematics aside, Excel is where we do the
heavy lifting. The screen capture below
is of an Excel spreadsheet that's set up to derive resistance and reactance values from frequency dependent
impedance magnitude and phase angle data. Columns A, B
and C are the experimentally obtained data and show the impedance magnitude
and phase angle at each test signal frequency. The table superimposed over
the spreadsheet shows the Excel complex number commands that correspond to
the cells in
columns D thru I. In this example one row is considered, row 3 (red
highlight). The spreadsheet provides the values for
a and
b shown in the expression for the
rectangular form of the impedance derived above. Note that early
versions of Excel require the Analysis Toolpak to be enabled prior to
working with complex numbers.
With
a and
b derived, a Nyquist plot can be
generated by selecting Column H as the Y-axis data and Column I as the
X-axis data keeping in mind that a +/-
b
really means +/-
jb.
This webpage, "Sparky" cartoon figure, text and
graphical content are
property of
North Reading Engineering, North
Reading, MA 01864 USA. No part of the above work may be copied and
published, in part or in total without written permission.
©
2018 John Warren
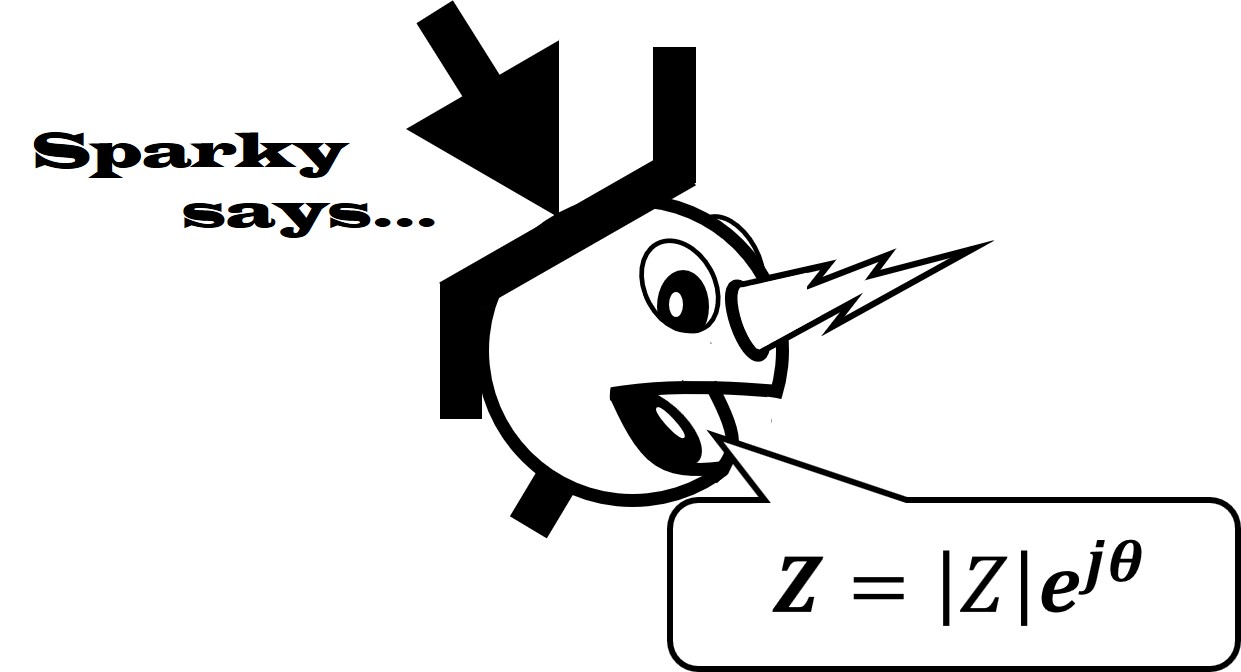


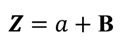


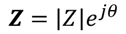 .
.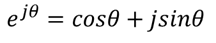
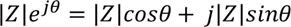
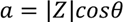
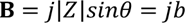 .
.